Noise suppression www.kovalevsky.de, last update: October 26, 2011		Let me know what you think
The simplest averaging filter  The fast averaging filter  The fast Gaussian filter  Sigma filter: the most efficient one  Comparison of different filters

The simplest averaging filter

The unweighted averaging filter calculates the mean gray value in a gliding square window of W*W pixels. The higher the window size W the stronger is the suppression of noise: the filter decreases the noise by the factor W. For the sake of symmetry W usually is an odd integer: 3, 5, 7, 9, 11 etc. The window coordinates (x+xx, y+yy) vary symmetrically around the current pixel (x, y): −W/2 ≤ xx ≤ +W/2 and −W/2 ≤ yy ≤ +W/2 with W/2 = 1, 2, 3, 4 etc.
The window lies at any image border partially outside of the image. In this case, the computation looses its natural symmetry because only pixels inside the image can be averaged. A reasonable way to solve the border problem is to take control of the coordinates (x+xx, y+yy) whether they point out of the image. In this case the summation of the gray values must be suspended and the divisor nS should not to be incremented.
The simplest slow version of the algorithm has four nested for-loops:

  int nS, sum;
  for ( int y=0; y < image0.Height; y++ ) //========================
  { for ( int x=0; x < image0.Width; x++ ) //=====================
    { nS=sum=0;
      for ( int yy=-W/2; yy <= W/2; yy++ ) //===============
      { if ( y+yy >= 0 && y+yy < image0.Height )
          for ( int xx=-W/2; xx <= W/2; xx++ )//==========
          { if ( x+xx >= 0 && x+xx < image0.Width )
            { sum+=image0.GetPixel( x+xx, y+yy );  nS++;
            }
          } //====== end for (int xx... ==================
        } //======== end for (int yy... ====================
      image1.SetPixel( x, y, (sum+nS/2)/nS);//+nS/2 for rounding
    } //============ end for (int x... ===========================
  } //============== end for (int y... =============================

where x, y are the indices of both image0 and image1 and xx,yy the indices of the pixels in the averaging window.
Then computation of each sum in the innermost for-loop needs W*W additions and W*W accesses to the image per one pixel, which is quite time consuming.

The fast averaging filter

The fast averaging filter solves the same problem, but it is much faster. The fast filter blurs the image as the simple filter does. Therefore its main application area is shading correction rather than noise suppression. The best filter for Gaussian noise suppression is the sigma filter described below. Using the following basic idea, it is possible to reduce the number of operations per pixel from W*W to ≈4:
The filter first calculates and saves the sum of the gray values in each column of W pixels, while the middle pixel of each column lies in the current row of the image. The filter then directly calculates the sum over the window having its central pixel at the beginning of a row, i.e. by adding up the sums saved in the columns. Then the window moves one pixel along the row, and the filter calculates the sum for the next location by adding the value of the column at the right border of the window and by subtracting the value of the column at the left border. It is necessary to check, whether the column to be added or subtracted is in the image. If it is not, the corresponding addition or subtraction must be skipped.
Applying a similar procedure to sum up the columns, the average number of additions/subtractions per pixel is reduced to ≈2+2=4.

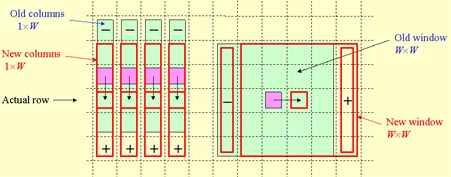When proceeding to the next row of the image, the filter updates the values of the columns by adding the gray value below the lower end and subtracting the gray value at the upper end of each column. Also in this case it is necessary to check, whether the gray value to be added or subtracted is in the image. As soon as the sum of the gray values in a window is calculated, the filter divides (with rounding) the sum by the number of pixels in the intersection of the window with the image and saves the result in the corresponding pixel of the output image.

The fast Gaussian filter The simple averaging filter produces a smoothed image, in which some rectangular shapes not present in the original image may be seen. These shapes arrive since the averaging filter transforms each light pixel to a homogeneously light rectangle of the size of the filter window. As soon as a pixel has an "outstanding" gray value, which differs from the values of adjacent pixels by a great amount, the rectangle becomes visible. This is an unwanted distortion. It can be avoided when using the Gaussian filter that multiplies the gray values to be added by values which decay with the distance from the centre of the window according to the Gauss law. The values of the Gauss law are floats less than 1. They can be calculated in advance and saved in a two-dimensional array. Then the gray values must be multiplied by these values and the sum of the products must be calculated. This procedure needs W2 multiplications and additions per pixel of the image to be filtered.   There is a possibility to obtain approximately the same results while using the knowledge of the statistics which says that the convolution of many equivalent probability distributions tends to the Gaussian distribution. The convergence of this process is so fast, that it is sufficient to calculate the convolution of only three "rectangular" distributions to obtain a good approximation. Thus to perform a Gaussian filtering of an image it is sufficient to filter the image three times by a fast averaging filter. This procedure needs 4*3=12 additions per pixel independently from the size of the window. If you are interested in the complete C++ code of the fast Gauss filter including border and color handling, write to kovalev@tfh-berlin.de Sigma filter: the most efficient one Both the averaging and the Gaussian filter blur the image. The averaging filter replaces each pixel of brightness B by a square of WxW pixels with the brightness B/(WxW). Thus steep edges of homogeneous regions become transformed to ramps of the width W. The idea of the sigma-filter consists in averaging only those gray values in a window, which differ from the gray value of the central pixel by no more than a fixed parameter "sigma". The pseudo-code: sum=0; number=0; M=Input(X,Y); for each pixel Input(x,y) in the window with the centre at (X,Y):   if (abs(Input(x,y)-M) < sigma) { sum+=Input(x,y); number++;}   Output(X,Y)=Round(sum/number); This naïve solution would work, but it would be rather slow: it needs in the worst case OPP=4*W 2 operations per pixel. Unfortunately, it is impossible to apply in this case the method used in the fast averaging filter since the procedure is non-linear. The procedure can be made faster due to the use of a local histogram. The histogram is an array, in which each element contains the number of occurrences of the corresponding gray value in the window. The sigma filter calculates the histogram for each location of the window by means of the updating procedure: gray values in the vertical column at the right border of the window are used to increase the corresponding values of the histogram, while the values at the left border are used to decrease them: OPP is the number of operations per pixel. 2*W is the number of operations necessary to actualize the histogram and 2*(2*sigma+1) is the number of operations necessary to calculate the sum of 2*sigma+1 values of the histogram and the corresponding number of pixels. Thus the overall OPP = 2*W+2*(2*sigma+1). Comparison of different filters The averaging and the Gaussian filter provide the most efficient suppression of the noise; however, they blur the image. The averaging filter with the window of W=(2*h+1) pixels transforms steep edges of homogeneous regions to ramps of the width W. The median filter is very popular. However, it is hardly known that it damages the image in a rather bad way: a median filter with the window of (2*h+1)*(2*h+1) pixels "bites off" a triangle of h*(h+1)/2 pixels from each corner of a rectangular region.   Original image   Filtered by median 5x5 Even more: median inverts an image with alternating black and white stripes of the width h (except at the border of the image), i.e. black becomes white and vice versa. The sigma-filter is the best one. When the parameters h and sigma are properly chosen, the filter preserves steep edges and does not destroy fine details of the image. The only drawback is the necessity to choose the parameters corresponding to a particular class of images. A class is characterized by the size of fine details and by the intensity of noise. By the way, there is a possibility, to automatically measure the intensity of noise and thus to automatically choose the value of sigma. Next figure shows the results of applying different filters to an image. If you are interested in details, write to kovalev@beuth-hochschule.de Download: Print version top of page: