As explained in the lecture "Introduction", topological notions of connectedness and of the boundary of a subset are important for image analysis. The widely used concept of m, n-adjacencies defines these notions not satisfactorily: different adjacencies for the foreground and background are only applicable for binary images. A subset has two boundaries: the inner and the outer ones. They do not satisfy the Jordan Curve Theorem.
A digital topological space must be locally finite which means that each space element must have a finite neighborhood, while in the classical Hausdorff-topology each neighborhood must be infinite. A space with infinite neighborhoods cannot be explicitly represented in a computer.

It is possible to define consistent digital topology while starting from classical topology. However, we have chosen another way, more comprehensible for practically oriented researchers. We have suggested a new set of axioms based on the notions of connectedness and boundary. We call a locally finite topological space satisfying our axioms an ALF space.

We have demonstrated that the neighborhood relation in an ALF space must be antisymmetric and transitive. Otherwise boundaries would be thick, i.e. consisting of two parallel running sequences of space elements. They would also contain gaps as explained below.

Smallest neigborhoods: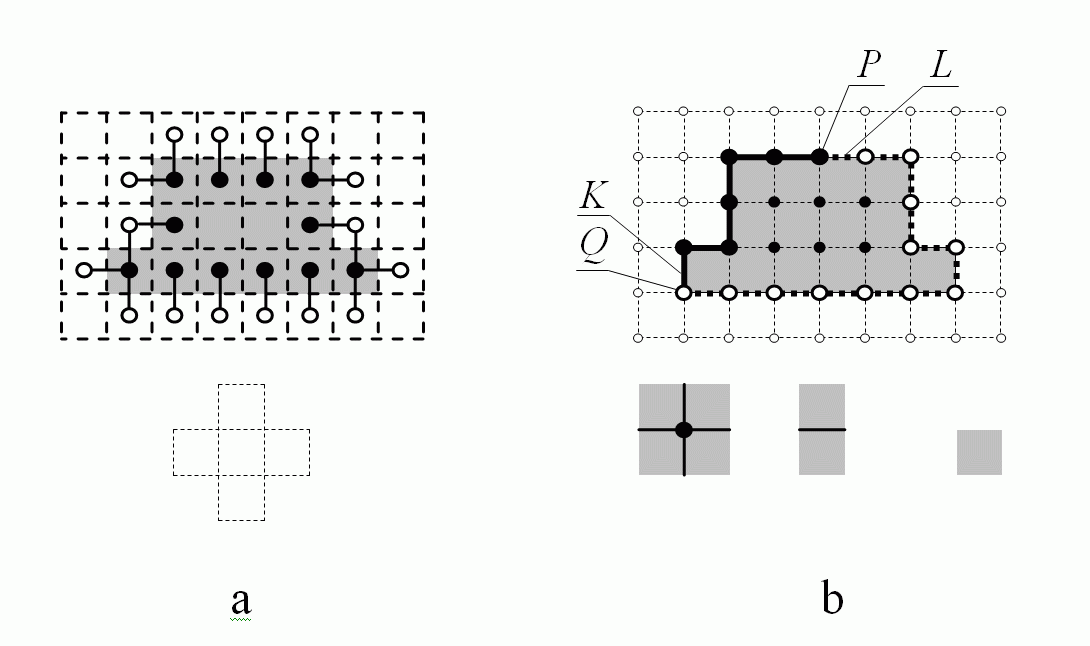

The smallest neighborhoods of different space element are shown in the above figure below the grid. They are different in a and b. In Fig. a the space S consists of squares only. The subset T is the set of gray squares. The symmetric relation N is the well-known 4-adjacency. Elements of the boundary Fr(T, S) are labeled by black or white disks. Squares with black disks belong to T, while those with white disks belong to S-T. In Fig. a each element of the boundary has at least one opponent. Pairs of opponents are shown by connecting lines. The boundary is thick.

In Fig. b the space consists of points (represented by disks), lines and squares. The boundary Fr(T, S) is represented by bold lines and big disks. The gray squares, solid lines and black disks belong to T; the white squares, dotted lines and white disks belong to S-T. The short solid line K∈T and the white point Q∈S-T belong to different subsets. Nevertheless, they are no opponents since Q does not belong to the smallest neighborhood SN(K). The same is true for the pair (L, P). Thus the boundary is thin. The boundary of T is the same as the boundary of its complement S-T.

Another important property of the boundary is, non-rigorously speaking, that it must have no gaps, which is not the same, as to say, that it must be connected. More precisely, this means, that the boundary of a boundary F is the same as F. For example, the boundary in the figure below has gaps represented by white disks. Let us explain this.

We have proved [1, 2] that the boundary Fr(F, S) is different from F= Fr(T, S) only if the neighborhood relation is non-transitive, which fact is important to demonstrate that the smallest neighborhoods satisfying our axioms are open subsets of the space.

There is a possibility to achieve that the boundary be thin for any subset of a space with a symmetric neighborhood relation: it is necessary to change the Definition FR of the boundary so that only elements of T may belong to the boundary of T. However, this possibility leads to different boundaries of T and of its complement S-T, which may be considered as a topological paradox and contradicts the classical definition of the boundary. Thus, the neighborhood relation in a space satisfying our axioms must be antisymmetric.

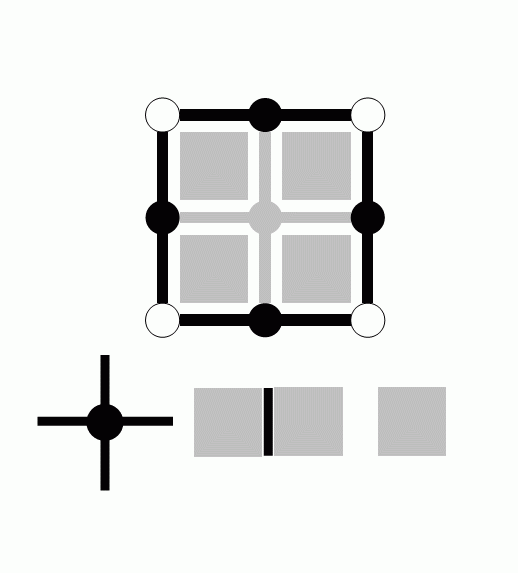
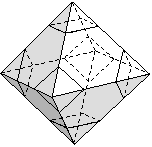
An n-dimensional LF space, in which the principal cells are isomorphic to translates of a single polytope and any two principal cells, which have a common incident cell of any dimension also have a common incident (n−1)-cell, is called a homogeneous completely connected space or an HCC space. If two principal cells have a common (n−1)-cell, then no topological contradiction as those explained at the beginning of this lecture and in the lecture 'Introduction' can occur. In a HCC space each pair of adjacent principal cells has a common (n−1)-cell. Therefore in an HCC space the adjacency pair (m, m), where m is the number of the principal cells adjacent to each principal cell, is consistent. The reader can easily see that the hexagonal grid is the only two-dimensional HCC space. It is known that the truncated octahedron (figure below) is the only "primitive" parallelohedron, i. e., at each of its vertices exactly 4 (generally: n+1) tiles of a suitable face-to-face-tiling come together. It has 14 faces. Parallelohedrons of this tiling are isomorphic to the principal cells of a 3D HCC space.

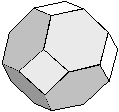The truncated octahedron

We have demonstrated [1] that the majority of the adjacency pairs are topologically contradictory. Even the few consistent pairs, (4, 8) and (8, 4) in 2D and (6, 26) and (26, 6) in 3D, have important drawbacks:

a)      They are only applicable in cases when there is only one subset of the space under consideration (and its complement). Thus they are not applicable, e.g., for colored images.

b)      Even in the case of a black-and-white image the structure created by an adjacency pair is topologically imperfect: thus, e.g. a 4-connected subset is full of holes due to the missing 0-cells. Consider e.g. an image with the (4, 8)-adjacency and the 4-connected dark subset of the figure below. It is topologically correct that the 0-cell between the pixels d and f belongs to the white subset making the pixels d and f disconnected and the pixels c and g connected.

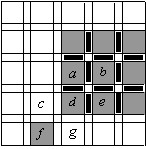
Holes in a 4-connected subset

However, it is not necessary, that the 0-cell between the pixels d and b belongs to the white subset. This makes the greater component of the dark subset not simply connected. The 0-cells incident to 4 pixels of T belong to the boundary of the dark subset and the boundary is disconnected, which is never the case for a simply connected subset of a topological space of dimension greater than 1. This drawback does not affect the desired connectedness; it can, however, lead to topological contradictions when solving more complicated topological problems. For example, a 6-connected "surface" in 3D has a lot of tunnels due to missing 1-cells.

c) The boundaries of subsets under an adjacency relation are either not thin (see above) or the boundary of a subset is different from the boundary of its complement, which is nonsense both from the point of view of topology and of the common sense.

d) The connectedness structure produced by an adjacency pair is no topological space at all since this structure is a property of a concrete subset of the space rather than that of the space. The connectedness changes when the subset changes.

What are the conclusions and the recommendations for algorithm design? We recommend not to use adjacency relations and to consider all topological and geometrical problems from the point of view of locally finite topological spaces (ALF spaces) or, even better, of complexes. The latter special case of an ALF space has some advantages due to the presence of the dimensions of cells. The dimensions of cells make the work with the topological space easier and more illustrative.

The usual objections against the use of complexes are the following:

a) Why should we use cells of lower dimension, which we don’t see on a display?

b) When using complexes, one needs much more memory space: 4 times or 8 times more in the 2D or in the 3D case correspondingly.

The objection because of visibility is not pertinent since the visibility has nothing to do with topology. For example, we all use in our work with 3D images the voxels. However, the voxels are not visible on the displays: what we see are the faces of voxels, i.e. the 2-cells, while voxels are 3-cells. Thus, e.g. the software "OpenGL", which is widely spread for representing 3D scenes, works only with faces of polyhedrons like triangles, squares, polygons and does not use three-dimensional bodies at all.

The second objection is pertinent only if one would try to allocate memory space for cells of all dimensions, which is almost never necessary. Cell complexes are a means for thinking about geometrical and topological problems rather than for data saving. It is possible to work with complexes, while saving in the memory only certain values assigned to the principal cells, like colors for the pixels, or densities for the voxels. Cells of lower dimensions are present as some kind of virtual objects only. Algorithms of this kind are described in [2].

In cases when the membership of cells of lower dimensions is important it can be defined by a "flat rate" face membership, i.e., a rule specifying the set membership of each cell as a function of the membership of the incident principal cells.

Consider the example of the figure below. Suppose, it is necessary to define the connectedness in such a way that both the white and the black "V" are connected. This is obviously impossible under any adjacency relation. The aim can be achieved by means of the following rule [2, page 190] for assigning membership labels to 1- and 0-cells.

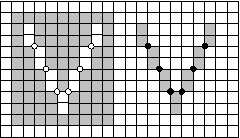
A white and a black V-shaped regions in one image, both connected
due to applying the EquNaLi rule

EquNaLi Rule:

A 1-cell gets the greatest label of the two incident pixels.

The label of a 0-cell c⁰ is defined as follows:

If SN(c⁰) contains exactly one diagonal pair of pixels with equivalent ("Equ") labels, then c⁰ gets this label. If there are two such pairs but only one of them belongs to a narrow ("Na") stripe, then c⁰ gets the label of the narrow stripe. Otherwise c⁰ gets the maximum, i.e. the lighter ("Li") label of the pixels of SN(c⁰).

The latter case corresponds to the cases when SN(c⁰) contains no diagonal pair with equivalent labels or it contains two such pairs and both of them belong to a narrow stripe.

To decide, whether a diagonal pair in SN(c⁰) belongs to a narrow stripe it is necessary to scan an array of 4x4 pixels with c⁰ in the middle and to count the labels corresponding to both diagonals. The smaller count indicates the narrow stripe.

Another important problem is that of using completely connected spaces. It is not correct to think that we need some special scanners or other special hardware to work with a hexagonal 2D space or with a 3D space tessellated by truncated octahedrons. It is possible to use as ever the standard orthogonal grids. The only thing, which must be changed is the definition of the incidence and hence that of the connectedness.

Consider the example of the hexagonal 2D space.

	a		b		c		d

A hexagonal grid, a transformed rectangular grid, a rectangular grid with 6-adjacency
and the "virtual" cells, transforming each pixel to a hexagon

Figure a shows a hexagonal grid. In the figure b we see the transformed rectangular grid, in which the upper left corner of each rectangular pixel is replaced by a slanted edge. The original rectangular grid is shown figure c. The arrows show the only six pixels, which should be considered as adjacent to the shaded pixel. If it is necessary to take cells of lower dimensions in consideration, then two 0-cells and three 1-cells must be assigned to each pixel, as shown in figure d. Thus two virtual 0-cells and one virtual 1-cell correspond to each vertex of the grid. The remaining two 1-cells correspond to the edges of the grid. All five faces assigned to a pixel have the same coordinates as the pixel. They can be distinguished by their types only. If it is necessary to assign a label to each 0-cell and to each 1-cell then 5 bits of the memory word assigned to the pixel can be used for these cells. The rest of the memory word can be used for the label or for the color of the pixel. It should be stressed once more, that the 6-adjacency realized by this data structure may be used for multicolored images and causes no topological paradoxes.

A similar data structure can be easily developed for the 3D standard grid to realize the 14-adjacency corresponding to the only 3D HCC space (see above).

We have suggested a new set of natural axioms of digital topology and have demonstrated, that they define a space, which is a particular case of a classical topological space. This fact serves as an explanation, why the key object of the classical topology, the system of open subsets, must have the properties formulated as the classical axioms: these properties are necessary (but not sufficient) to define the connectedness through neighborhoods and the boundary of a subset T as a thin subset, which is the same for a subset T and for its complement.

The paper [1] demonstrates how the (a, b)-adjacency relations commonly used in computer imagery can be brought into accordance with the connectedness of a topological space. It was demonstrated that in spaces of any dimension n only those pairs (a, b) of adjacencies are consistent, in which exactly one of the adjacencies is the "maximal" one corresponding to 3ⁿ-1 neighbors. Even the consistent pairs have important limitations: they are not applicable for multicolored images and they cannot correctly represent topological properties of subsets. We suggest to use instead the concept of ALF spaces, while considering space elements of lower dimensions as "virtual" objects, which need not be saved in the memory. This attitude makes it possible to apply consistent topological definitions and algorithms to images represented in standard grids. The notion of homogeneous completely connected spaces is introduced, and it has been demonstrated, that there is only one such space of dimension 3; it is isomorphic to the tessellation by truncated octahedrons, each of which has 14 adjacent octahedrons.

We have shown how locally finite spaces, especially cell complexes and completely connected spaces, can be applied to computer imagery, while using standard orthogonal grids.

[1] V. Kovalevsky, "Axiomatic Digital Topology". Journal of Mathematical Imaging and Vision. vol. 26, pp. 41-58, 2006.

[2] V. Kovalevsky, "Geometry of Locally Finite Spaces". Monograph, Berlin 2008.