Convex Hulls
Copyright © by V. Kovalevsky, last update: October 24, 2011


Let me know
what you think
 Definition
Definition Idea of the Algorithm
Idea of the Algorithm The Algorithm in the 3D Case
The Algorithm in the 3D Case References
References| Home | Index of Lectures | << Prev | Next >> | PDF Version of this Page |
Convex HullsCopyright © by V. Kovalevsky, last update: October 24, 2011 |
 |
 Let me know what you think |
 Definition Definition Idea of the Algorithm Idea of the Algorithm The Algorithm in the 3D Case The Algorithm in the 3D Case References References |
 |
| A point P is a convex combination of the points xj (j=1, 2, ..., n), if P= | where the sum of the non-negative values ti is equal to 1. |
We describe the surface of the 3D convex hull by a 2D cell list (see the section "Block Complexes and Cell Lists" above). The algorithm starts with producing a list L of all local corners. It chooses four non-coplanar points of L and produces the cell list of the spanning tetrahedron. This is the "current hull" CH which will be completed step by step to the convex hull of L. The algorithm tests each local corner of L while finding all faces of CH which are "visible" from the local corner. The face F of a convex polyhedron is visible from a point P if P lies in the outer open half-space bounded by F, i.e. if the scalar product (N, W) of the outer normal N of the face F and the vector W pointing from an arbitrary point Q in F to P, is positive. If the scalar product is negative, then F is said to be invisible from P. If the scalar product is equal to zero, then F is said to be coplanar with P. If one or more faces are visible, then the polyhedron is being extended by the point P and some new faces. Each new face connects P with one of the edges of the boundary of the set of visible faces. A new face is a triangle having P as its vertex and one of the edges of the said boundary as its base. All triangles are included in the cell list of the current hull, while all visible faces are removed from the list. Also each edge incident to two visible faces is removed. When all local corners are processed in this way then the convex hull is ready. The figure below explains the idea of the algorithm by a 2D example. The starting triangle is drawn in black lines. Polyhedrons in red and blue are following.
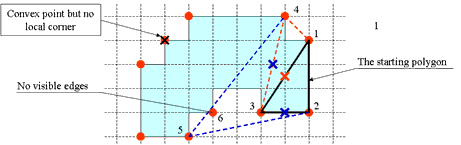 |
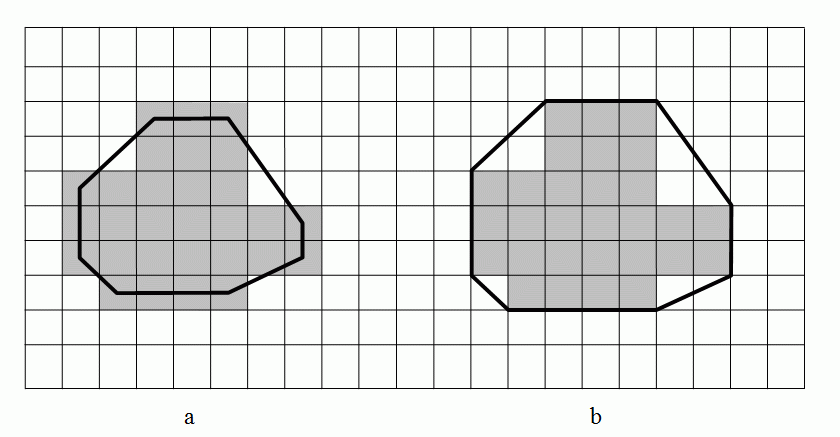
The following figure shows an example of a 3D body and its convex hull.
 |  |
| A 3D object | Its convex hull |
1. Make the list of all local corners.
2. Find four local corners which are not coplanar and construct the cell list of the tetrahedron.
This is the current hull.
3. For each local corner P find all visible faces of the current hull. If there
are no such faces then P lies inside the hull and should be skipped. Otherwise connect
P with all edges of the visible area, put P and the new triangles into the list and
delete the visible area.
4. Repeat item 3 for all local corners.
5. If there are some coplanar triangles merge them to polygons.
End of algorithm.
[1] V. Kovalevsky and H. Schulz, Convex Hulls in a 3-dimensional Space, In: Klette, R. and Zunic, J. (Eds): Lecture Notes in Computer Science, Vol. 3322, (2004), pp. 175-191...
[2] V. Kovalevsky: Geometry of Locally Finite Spaces, Monograph, Berlin 2008.
Download: Print version| top of page:
|
Last update: October 24, 2011