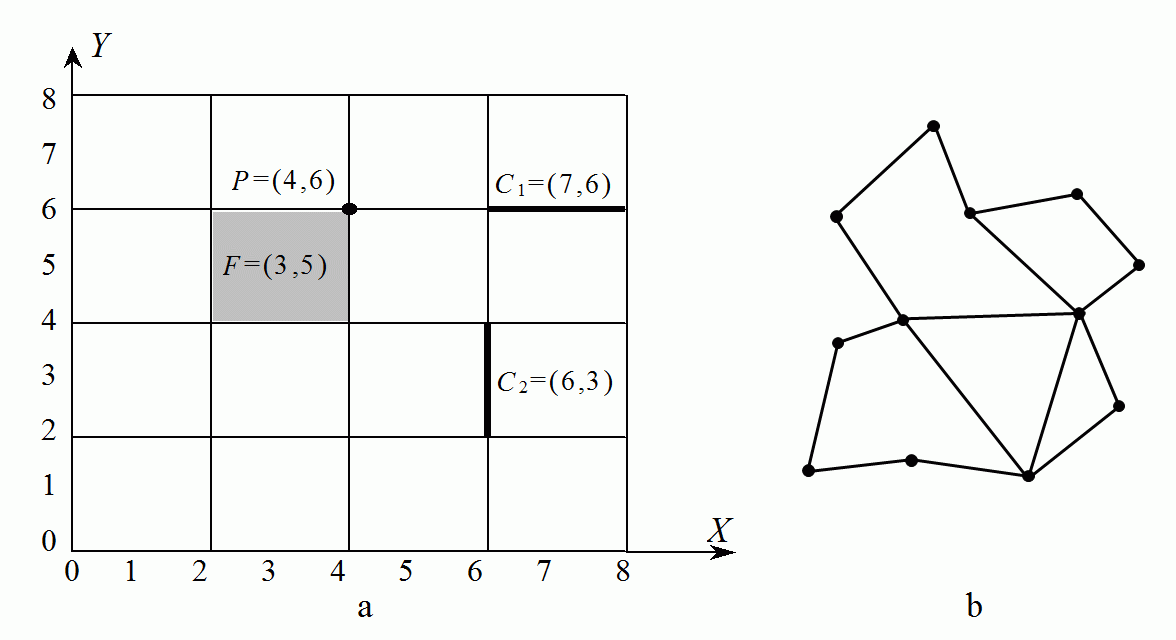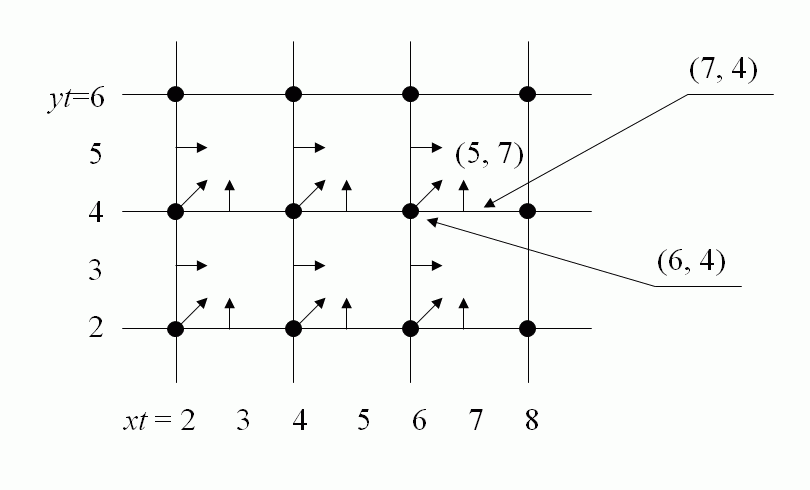Why is Topology Important for Image Analysis?
We need in image analysis and in computer graphics the notions of connected subsets, of adjacent subsets, of boundaries, of the
interior and exterior etc. All these are topological notions. Topology may be considered as the geometry of a rubber sheet: all
mentioned properties of subsets being drawn on a rubber sheet remain preserved when one pulls the sheet without tearing it.
A mathematician would say that topological properties are invariant under continuous transformations of the space.
The general topology considers spaces in which even the smallest neighborhood of a point contains infinitely many other points.
It is obvious that such a space (and even the smallest part of it) cannot be explicitly represented in a computer. Therefore we need
the topology of the so called locally finite spaces whose elements have neighborhoods containing a finite number of elements.
In the 1970th Rosenfeld has suggested to consider in an digital image the 4- and the 8-adjacency of pixels. He defined an
m−path as a sequence of m−adjacent pixels, m being 4 or 8. He also introduced the m-connectivity:
a subset S of pixels is m-connected if it contains for any two pixels of S an m-path from one of the pixel
to another.
 | | We need the notions of:
− connected subsets
− boundary of a subset
− adjacent subsets
− interior and exterior etc. |
The m−adjacency in the digital 2D space
 | | The well−known Jordan property of a simple curve:
The curve must separate the rest of the space in exactly two components.
left: A simple 4−curve makes tree components
right: A simple 8−curve makes one component
The "mixed" (8, 4)−adjacency is applicable to binary images only. |
The Connectivity Paradox of the m−Adjacency
 | |
Under the 4−adjacency both the green and the red subset are disconnected.
Under the 8−adjacency both the green and the red subset are connected which is paradox.
A consistent connectivity may be defined when the membership of the white point in the middle in one of the subsets is specified.
|
The notion of m−connectivity turns out to be contradictory: it is well−known (as the Jordan theorem) that a simple closed
curve in the plane subdivides the rest of the plane into two connected parts. Under the m−adjacency a simple closed curve is
a sequence of pixels, in which each pixel is m−adjacent to exactly two other pixels. There exist under the 4−adjacency simple
curves that subdivide the rest of the plane into more than two components. Under the 8−adjacency a simple closed curve does not
subdivide the rest of the plane at all.
When considering four pixels having all a common corner one may see the connectivity paradox ones more: under the 4−adjacency each of
the two "diagonal" pairs of pixels is disconnected; under the 8−adjacency they are both connected. Thus one 8−path crosses
another such path while the two paths have no common elements. Rosenfeld has suggested to consider a "mixed" adjacency:
the 8−adjacency for the foreground of an image and the 4−adjacency for the background or vice versa. This suggestion has removed the
connectivity paradox for binary images. However, it remains for multilevel images. Besides that, a mixed (m,n)−adjacency does
not define a topology of the space but rather a "topology" of concrete subsets of the space: it changes if the subsets
change.
The solution of this paradox consists in considering besides the pixels another kind of space elements − the points and the cracks.
The membership of the point defines the connectivity of pairs of adjacent pixels.
 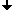 |
Boundaries under the (m,n)-adjacency
One of the most important topological notions is that of a boundary. The topological boundary (or frontier) of a subset T of
the space S is the set of all space elements whose each neighborhood contains both elements of T and of its complement
S−T. In the topology of continuous spaces the boundary of a subset of the plane is a curve. It is thin, i.e. its
area is equal to zero. The boundary is the same for T and for its complement S−T since the above definition
is symmetric with respect to T and S−T.
When considering the neighborhood of a pixel P as the set of all pixels m-adjacent to P (including P itself)
then the boundary becomes a thick stripe whose width is equal to two pixels. When, however, we change the definition so that the
boundary of T contains only pixels of T then we arrive at two different boundaries: the boundary of T is then
different from the boundary of the complement S−T. This is also a topological paradoxon.
The solution of this problem consists in considering neighborhoods based on an antisymmetric binary relation: if the space
element a belongs to the smallest neighborhood of the element b then b does not belong to the smallest neighborhood
of a. A topological space with such neighborhoods is a cell complex if also the dimension of its elements are defined.
It follows from the above mentioned antisymmetry
that the space must contain elements of different smallest neighborhoods and therefore elements of different kind.
 | | Examples of boundaries under the (m,n)-adjacency
The m-boundary of a subset T is the set of elements (of T) that have m-neighbours in the complement of
T.
left: The 4-boundary is not 4-connected
right: The 8-boundary is not a simple curve
The boundary of a subset is different from that of its complement!
If we delete "of T" in the definition of the boundary, it becomes thick. |
How to overcome these difficulties?
Abstract Cell Complexes
Definition AC: An abstract cell complex C=(E,B,dim) is a set E of abstract elements (cells) provided with an
antisymmetric, irreflexive and transitive binary relation B⊂ExE called the bounding relation, and with a
dimension function dim: E→I from E into the set I of non-negative integers such that
dim(e')<dim(e") for all pairs (e',e")∈B.
If (a,b)∈B then it is usual to write a<b or to say that the cell a bounds the cell b.
Such cells are called incident to each other.
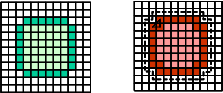
Examples of AC complexes:
 | |  | |
 |
2-dimensional
non-cartesian | | 2-dimensional
cartesian |
| 3-dimensional |
A digital image is to be considered as a 2-dimensional complex. It contains cells of three kinds: namely the cells of dimensions
from 0 to 2. The 2-dimensional cells, or 2-cells, are the pixels, the 1-cells are called cracks or edges and the 0-cells
are the points or the vertices. A crack may bound a pixel, but not vice versa. A point may bound a crack and a pixel.
Definition OP: A subset OS of cells of a subcomplex S of a complex C is called open in S if it
contains all cells of S bounded by cells of OS. An n-cell cn of an n-dimensional complex
Cn is an open subset of Cn since cn bounds no cells of Cn.
Definition SON: The smallest subset of a set S which contains a given cell c of S and is open in S
is called the smallest (open) neighborhood of c relative to S and is denoted by SON(c,S).
The SON of a pixel is the pixel itself. SONs of other cells are shown in the following figure.
Definition CL: A subset CS of cells of a subcomplex S of a complex C is called closed in S if it contains
all cells of S bounding the cells of CS. An 0-cell c0 of an n-dimensional
complex Cn is a closed subset of Cn since there are no cells bounding
c0. The smallest subset of a set S which contains a given cell c of S and is
closed in S is called the closure of c relative to S and is denoted by Cl(c,S).
Two cells are called incident to each other if they are either identical or one of them bounds the other.
Connectivity in cell complexes is defined by means of incidence paths:
An incidence path is a sequence of cells in which each two subsequent cells are incident to each other.
A subset S is connected if for each two cells of S there exits in S an incidence path containing these cell.
The topological boundary (frontier) of a subset T of a complex C is defined as in the general topology: it is the set of all cells whose smallest neighborhood contains both cell s of T and of its complement C−T.
The boundary of a subset of a 2D space contains no pixels since the SON of a pixel is a singleton consisiting of a single cell and
cannot contain cells of T and of C−T. Thus the boundaries in complexes are always thin.
| Closures and Smallest Neighborhoods of Cells |
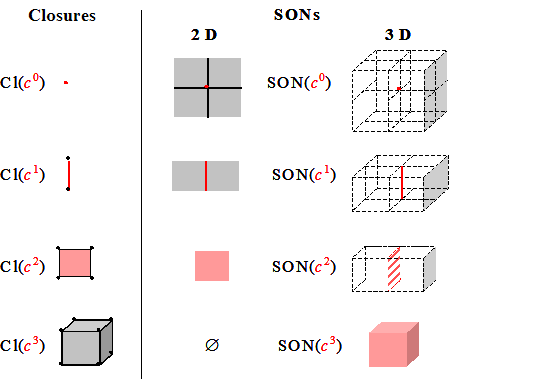 |
Connectivity
An incidence path is a sequence of cells in which any two subsequent cells are incident to each other. A set S is connected
if for any two cells of S there exists in S an incident path including these two cells.
The membership of cells of lower dimensions can be defined either explicitly or by means of an overall membership rule.
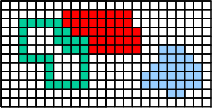
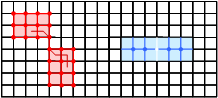 | | Example:
The red subset is connected, the blue one
is disconnected. |
The Topological Boundary of a Set
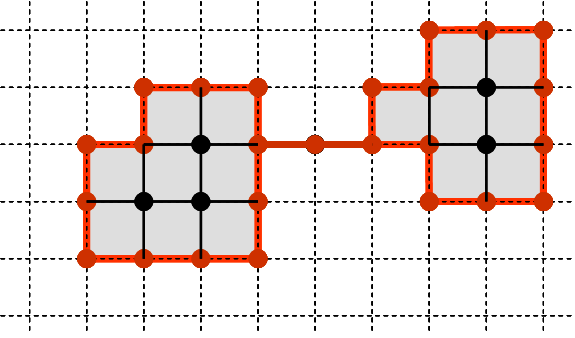 | | Red lines and dots show the
topological boundary (frontier) of the gray-and-black complex. The boundary contains no principal cell (i.e. no n-cells in an
n-space; no pixels in the 2D space).
Definition: The boundary Fr(S, C) of a subset S⊂C is the set of all cells c∈C whose smallest
neighborhood SON(c, C) contains cells both of S and of its complement C−S.
The well-known notion of the m-boundary is contradictory and should not be used. |
The Open Boundary of a Set
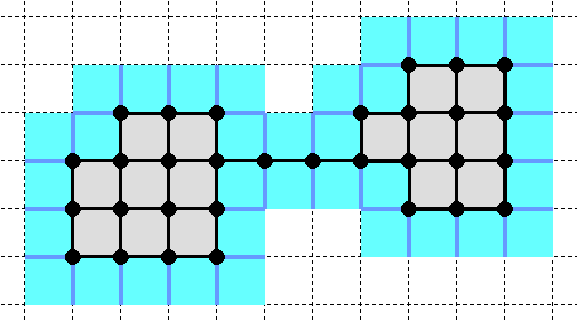 | |
Blue lines and squares show the open boundary of the gray-and-black complex. It contains no 0-cells.
Definition: The open boundary OP(S, C) of a subset S of C is the set of all cells c∈C whose
closure Cl(c, C) contains cells both of S and of its complement C−S.
|
 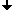 |
Cartesian Complexes
A one-dimensional complex which is a sequence of alternating 0-cells and 1-cells may be considered as a coordinate axis of a
multidimensional Cartesian complex. The set of cells of a multidimensional Cartesian complex is the Cartesian product of the sets of
cells of the axes. This means that a cell of an n-dimensional Cartesian complex Cn is an
n-tuple of the cells of the axes.
The bounding relation in Cn is deduced from the bounding relations of the axes. The dimension of a cell of
Cn is the sum of the dimensions of the factor cells.
It is possible to assign integer numbers to the subsequent cells of the coordinate axes. These are the combinatorial coordinates in
the space Cn. A location of a cell c∈Cn in the space is characterized by an
n-dimensional vector whose components are the combinatorial coordinates of the factor cells of c in the
corresponding axes.
Combinatorial coordinates make the development of algorithms in digital geometry easier and more comprehensible.
Samples:
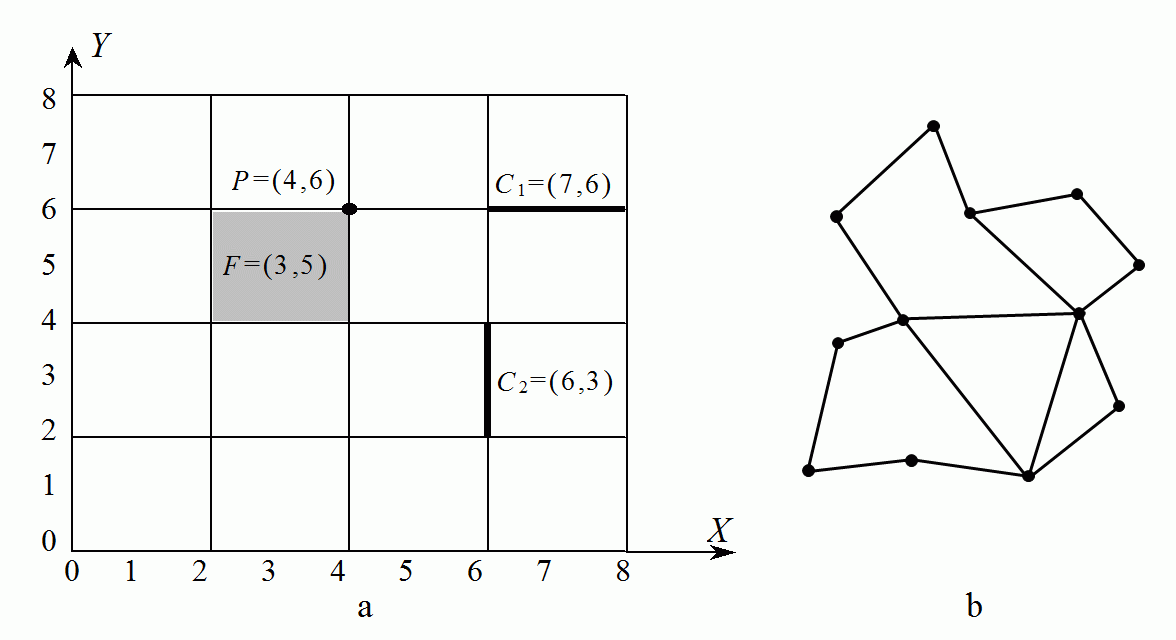 | A Cartesian (a) and a general (b) complex.
P in (a) is a 0-cell (a point),
C1 and C2 are 1-cells (a horizontal and a vertical crack),
F is a 2-cell ( a pixel). |
Data Structures:
 | left: Standard grid �well suited to store images
right: Combinatorial grid well suited for geometrical calculations
Both grids should be used simultaneously, the transition from the combinatorial grid (xc, yc) to the standard one
(xs, ys) being very simple:
xs=int(xc/2); ys=int(yc/2); |
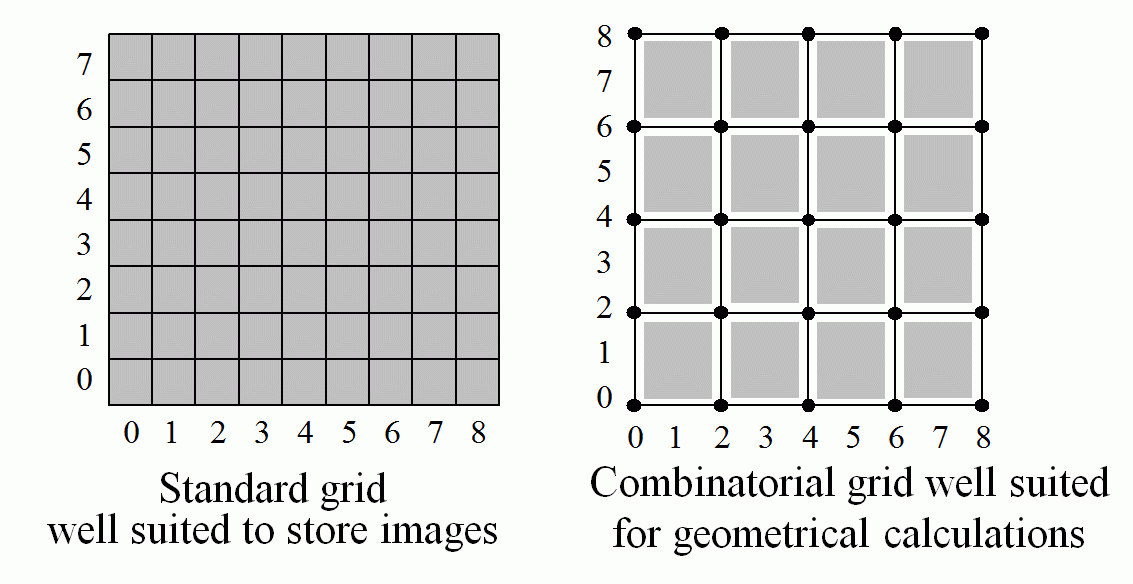
The coordinate assignment rule:
 | Cells of lower dimension have in standard grid the
same coordinates as the
corresponding principal cell, i.e. the cell of the greatest dimension. The correspondence is defined by the assignment rule and is
shown in the figure. Using the assignment rule gives the possibility to work with cells of lower dimensions in the standard grid.
xs=xc/2;
ys=yc/2; |
If you are interested in theoretical details read the lection "Axiomatic Digital Tology" below
and take the book: 'Geometry of Locally Finite Spaces'.
Download: Print version
Last update: October 24, 2011


 Why is Topology Important for Image Analysis?
Why is Topology Important for Image Analysis? The m−adjacency in the digital 2D space
The m−adjacency in the digital 2D space Boundaries under the (m, n)−adjacency
Boundaries under the (m, n)−adjacency Abstract Cell Complexes
Abstract Cell Complexes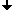 Connectivity
Connectivity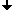 Cartesian Complexes
Cartesian Complexes