Straight Segments in Digital 2D Space Copyright © by V. Kovalevsky, last update: October 24, 2011		Let me know what you think
Definition and Properties of a DSS  Subdividing a curve into longest DSSs  Applications of the DSSs  Area and Perimeter  References

Definition and Properties of a DSS

We suggest to consider a digital straight segment (DSS) as a subset of the boundary of a part of a 2D image regarded as a cell complex, namely as a connected subset of the boundary of a half-plane. A half-plane is the closure of all pixels (2-cells) whose coordinates satisfy a linear inequality. Thus our DSS is a sequence of alternating 0- and 1-cells rather then that of pixels [1, 2, 3]. This kind of a DSS is important for image analysis since it gives the possibility to investigate geometrical properties of image parts whose boundaries can be represented as sequences of DSSs. Boundaries are precisely defined in cell complexes as sequences of cracks (1-cells) and points (0-cells).
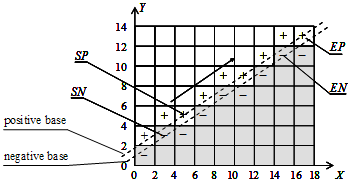
Each crack of a DSS bounds two pixels one of which lies to the positive side of the oriented crack and the other to the negative side. (The positive Y-axis of the coordinate system lies to the positive side of the positive X-axis). There exists a linear form H(x, y)=a⋅x+b⋅y+c which separates the set of all positive pixels from that of the negative ones: H(x,y)≥0 for the positive and H(x,y)<0 for all negative pixels. The form H(x, y) is called the standard separating form (SSF) of the DSS if
    1) its coefficients at x and y are mutually prime integers and
    2) H(x, y)=0 in at least two positive pixels or
    3) H(x, y)=−e in at least two negative pixels, where e=1 for the standard and e=2 for the combinatorial coordinates.
The set of positive pixels with H(x, y)=0 is called the positive base of the DSS.
The set of the negative pixels with H(x, y)=&minus:e is its negative base.

It has been proved [4] that the oriented cracks of a DSS have at most two different directions. They are evidently orthogonal to each other. The two other possible directions of cracks are called the prohibited directions of the DSS. It has been also proved that the values of the SSF H(x, y)=a⋅x+b⋅y+c for the positive pixels of a DSS lie in the interval:
         0 ≤ H(x, y) ≤ max(|a|,|b|)−e;
and for the negative pixels in the interval:
         −max(|a|,|b|) ≤ H(x, y) ≤ −e.
These properties are used for fast recognition of DSSs during the tracing of the boundary of a region.

The subdivision of a boundary into longest DSS starts at some crack C of the boundary. A single crack is a DSS. Its SSF is H(x, y)=a⋅(x−x₀)+b⋅(y−y₀) where (x₀, y₀) is the positive pixel of C and (a, b) is a unit vector orthogonal to C.
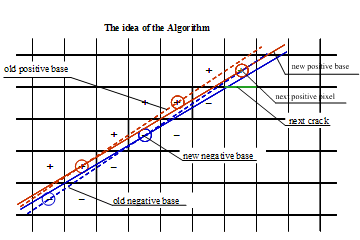
The algorithm finds for each next crack C of the given boundary its positive and the negative pixels, calculates the values of the SSF and checks whether they are in the intervals mentioned above. If they do then C belongs to the current DSS and its recognition can be continued. If they do not and the deviation form the boundary of the interval is minimal (i.e. its absolute value is equal to e) then the parameters of the current DSS must be corrected. If the deviation is greater than e then C does not belong to the current DSS. The starting point of C is then the last point of the DSS and the recognition of the next DSS must be started at this point with the crack C.

	Examples of a half-plane and of a DSS in combinatorial coordinates: Definition: A digital straight segment (DSS) is any connected subset of the frontier of a digital half-plane
	The standard separating form H(x, y) ≥ 0 for the positive pixels

Subdividing a Curve into Longest DSSs

Verbal description of the Algorithm:
Given are the coordinates of each crack C of the given digital curve and its direction DIR. For each crack C do:
1. Find the positive P and the negative N pixel incident to the crack C.
2. At the beginning of a DSS find
  2a. the prohibited directions,
  2b. the endpoints StartP, EndP, StartN, EndN of the bases and
  2c. the parameters a, b of the separating form SSF: H(x, y) = a⋅x+b⋅y+c=a⋅(x−x₀)+ b⋅(y−y₀)
3. If the direction DIR is not prohibited calculate the values HP and HN of H(x, y) for the pixels P and N.
4. The following steps of the Algorithm are the decisive ones:
  If HP<−e or HN>0 then stop: the running DSS ends at the starting point of C.   Save the point and start the next DSS.
  (The constant e is equal to 2 in topological coordinates and to 1 in standard coordinates).
  If HP=0 then set EndP=P: P lies on the positive base which must be prolonged.
  Otherwise, if HP=−e then redefine both bases while setting EndP=P; StartN=EndN and redefine the parameters a and b of H(x, y) according to the redefined bases.
  Do similar tests for the value of HN:
  If HN=−e then set EndN=N: N lies on the negative base which must be prolonged.
  Otherwise, if HN=0 then redefine both bases while setting EndN=N; StartP=EndP and redefine the parameters a and a of H(x, y) according to the redefined bases.
  Take the next crack.

Pseudocode of the Recognition of a DSS:

typedef struct { int x,y;} iPoint;
iPoint ToPos[4]={{0,1},{-1,0},{0,-1},{1,0}};  // positive pixel of the DSS
iPoint Param[4]={{1,0},{0,1},{-1,0},{0,-1}};  // coefficients of the SSF for single crack
iPoint EndN, EndP, StartN, StartP;
int a, b, e=2, CC, Prohibit1, Prohibit2;
iPoint Vertex[1000];    // vertices of the DSS
int Last[100], iPoly=0, iVert=0, nVert=0;   // Last[i] is the index in "Vertex"
                                            // of the last vertex of the ith polygon.
int Opposite(int dir) {  return (dir+2)%4;}
int GetH( iPoint V )  {  return a*(V.x-StartP.x)+b*(V.y-StartP.y);}

void Ini() { CC=0;  Prohibit1=Prohibit2=-1; }

int Reco(iPoint Crack, int dir)
{  iPoint N, P;       // N is the negative pixel of Crack
    P.x=Crack.x+ToPos[dir].x;   P.y=Crack.y+ToPos[dir].y;
    N.x=Crack.x-ToPos[dir].x;   N.y=Crack.y-ToPos[dir].y;
    if (CC==0) //------------- "CC" is the number of the tested cracks ---------
    {  Prohibit1=Opposite(dir);  Prohibit2=-1; CC=1;
       StartP=EndP=P;   StartN=EndN=N;    // Param is a unit vector along "dir"
       a=-Param[dir].y;  b=Param[dir].x;        return 0;
    } //--------------------------------- end if (CC==0) -----------------------
    if (dir==Prohibit1 || dir==Prohibit2) return 1;
    if (dir!=Opposite(Prohibit1) && Prohibit2==-1) Prohibit2=Opposite(dir);
    if (CC==1) //---------------------------------------------------------------
    {   EndP=P; EndN=N; CC=2;
        if (Prohibit2==-1) return 0;   // only one direction
        if (EndP.x==StartP.x && EndP.y==StartP.y)
        {  a=-(EndN.y-StartN.y)/e;  b=(EndN.x-StartN.x)/e; }
        else
        {  a=-(EndP.y-StartP.y)/e;   b=(EndP.x-StartP.x)/e;}
        return 0;     // any two allowed cracks compose a DSS
    } //--------------------------------- end if (CC==1) -----------------------

  int HP=GetH(P);  int HN=GetH(N);  // the values of the SSF "H"
  if (HP<-e || HN>0) return HP;     // not a DSS
  if (HP==0)  EndP=P;   // the positive base must be prolonged
  else
      if (HP==-e)
      {  EndP=P;   StartN=EndN;   // the parameters of the DSS changes
         a=-(EndP.y-StartP.y)/e;  b=(EndP.x-StartP.x)/e;
      }
  if (HN==-e) EndN=N;   // the negative base must be prolonged
  else
      if (HN==0)
      {  EndN=N;   StartP=EndP;   // the parameters of the DSS changes
         a=-(EndN.y-StartN.y)/e; b=(EndN.x-StartN.x)/e;
       }
  return 0;
} //************************** end Reco *******************************

If you are interested in details write to kovalev@beuth-hochschule.de

Applications of the DSSs

DSS can be applied for the following purposes:

This gray value image of 390⋅480=187200 pixels with 32 gray levels was encoded with 60080 bytes. Thus the compression rate was about 3.1. This is the image exactly reconstructed from the code [2].

Fast encoding of an image by DSS polygons and recognizing all disk-shaped objects. This binary image of 832⋅654 pixels was encoded by DSSs. 57 disk-shaped objects were recognized within < 20 msec [4](page 220).

Area and Perimeter

A good estimate of the area of a subset S in a 2D digital image is the number of pixels in S. When increasing the resolution (i.e. making the pixels smaller and multiplying the number of the pixels with the area of a single pixel) the estimate tends to the area of the original continuous image. However, the number of cracks in the boundary of a subset is not a good estimate of the perimeter: when rotating the original image by 45° the estimate may change by up to 41%! When increasing the resolution the estimate does not change at all!
A good estimate of the perimeter is the sum of the lengths of the longest DSS in the boundary of the subset. It tends to the perimeter of the original image at least if S is convex or is a polygon whose inner angles are not too small [3].
The length of a DSS is the Euclidean distance between its end points: L= sqrt( (xe−xs)²+(ye−ys)² );
where (xs, ys) are the coordinates of the starting and (xe, ye) that of the end point of the DSS.

Pixels and Cracks of a Rotated Object:

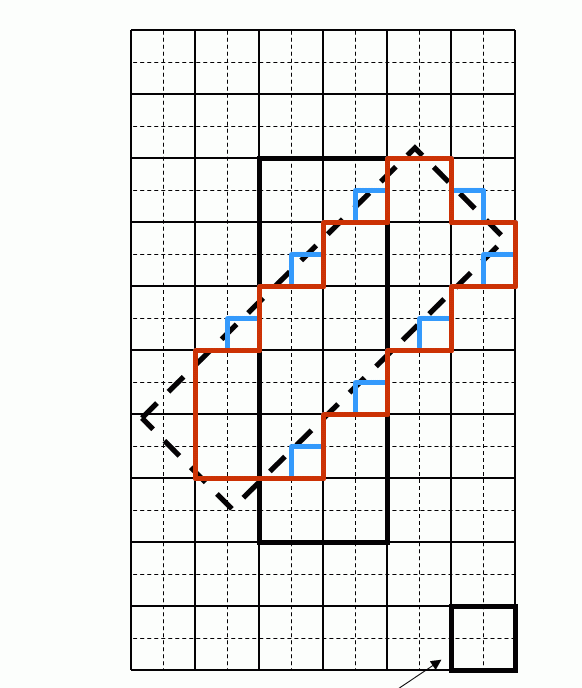Black and red lines represent large pixels while blue lines represent small pixels. The number of pixels and cracks in the black line:      6⋅2=12 pixels; 16⋅1=16 cracks                                       The same in the red line:   12⋅1=12 pixels; 20⋅1=20 cracks                                     The same in the blue line:   48⋅0.25=12 pixels; 40⋅0.5=20 cracks

Example of Defining the Perimeter

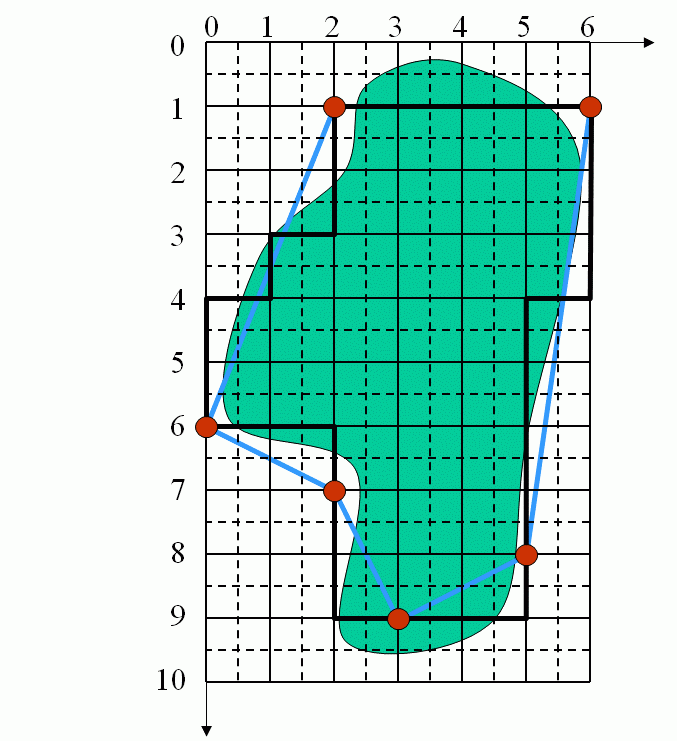Coordinates of the DSS end points: (2,1)   (0,6)   (2,7)   (3,9)   (5,8)   (6,1)   (2,1) ;                  Corresponding lengths:        5.38 +2.24 +2.24 +2.24 +7.07 + 4.0 = 23.17

    References

top of page:

Last update: October 24, 2011